第3回 新刊算法起を読む:2
いよいよ、具体的に解法を見ていきます。
前回の(注2-1)で示しましたが、当時(江戸時代)の間と尺との換算率は、0,65でした。つまり「1間 = 6尺5寸」です。だから尺以下の数を間に換算するには、0.65で割る必要があります。
これが現代語訳中の初めからの4行にあたります。まず一辺の長さを間の長さの単位に統一したのです。
この一辺の長さを二乗したのは、正方形の面積を求めるためというのは分かりますね。 17.32×17.32=299.9824 ≒300
つまり300坪となります。 1間四方の正方形の面積は1坪ですので、上の場合、 間(一辺の単位)×間(一辺の単位)=坪(面積) となるんですね。
次は面積の坪を反への換算注3-1です。 当時は、1反=10畝=300坪 でした。 つまり、300坪=1反 です。 ちなみに、1坪=1歩(ぶ)=1間×1間 です。
ところで、最後の現代語訳にある「田の法3で割る注3-2」というのは、歩の単位の値を、畝や反の値に直すのに、30または300で割って求めるので、この「3」を「田の法」と言ったのです。所謂、定数ですね。
なお、1行目の「17間2尺超えて8分」の「超えて」は、その位が空位つまり「0」であることを表しています。
では、続きの文を示しましょう。今回の問題です。今回は複数用意しました。ゆっくり解いてみてください。
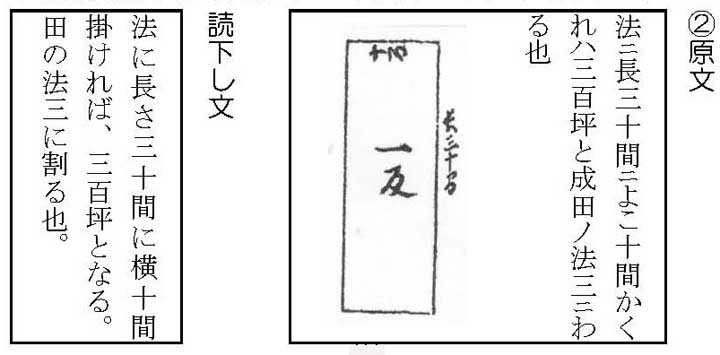
 ここでは、原文に「長三十間」とあります。「長注3-3」とは、この問題での長い方の辺の長さをいいます。この図形では縦長の長方形なので、縦の長さが「長」にあたります。
ここでは、原文に「長三十間」とあります。「長注3-3」とは、この問題での長い方の辺の長さをいいます。この図形では縦長の長方形なので、縦の長さが「長」にあたります。
続いて、第3問です。
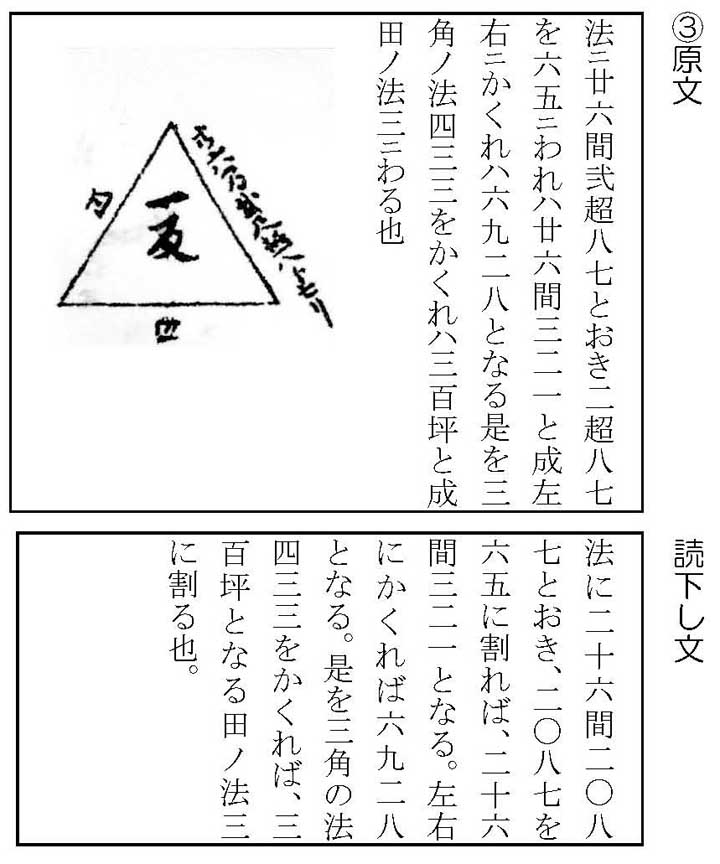
もう一つ、原文の4行目「三角ノ法四三三注3-4」が出てきています。前回は「田の法3で割る」でしたが、今回は少し違うようです。四角形の面積を正三角形の面積に換えるための定数だと考えてください。前回同様、数字が並んでいるだけですので、もちろん小数点以下の数字となっていますよ。
今回のは結構易しいので、もう1問出しましょう。
この文では、「0.65」で割っています。前回とは逆の換算ですね。
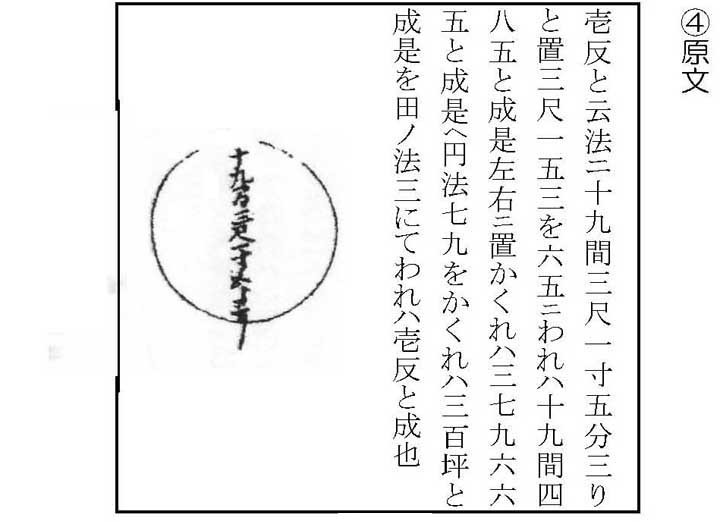
もう1つ、「円法0.79注3-5」が出てきました。これは円の直径を1辺とした正方形の面積を、円の面積に換える定数と考えてください。
そして、最後にはやはり「田の法3」が出てきました。覚えておられますか。
では、解いてください。前回同様、私の解法は、次回に掲載いたします。
注3-1:長さ・面積・体積・重さの換算
長さ
町:1町=60間(約108m)
間:1間=6尺5寸(約1.8m)後に6尺に
尺:1尺=10寸(約30.3cm)
寸:1寸=10分(約3cm)
分:1分=10厘(約3mm)
厘:1厘=10毛(約0.3mm)
毛:1毛=10糸
面積
町歩:1町歩=10反歩(約99.2アール =9920m2)
反 :1反 =10畝(約992m2) =300坪
畝 :1畝 =30歩=30坪(約99.2m2)
歩 :1間四方=1坪(約3.3m2)
坪 :1間四方=1歩(約3.3m2)
体積
石:1石=10斗(約180ℓ)
斗:1斗=10升(約18ℓ)
升:1升=10合(約180cc)
合:1合=10勺(約18cc)
勺:1勺=10抄(約1.8cc)
重さ
貫 :1貫=1000匁(約3.75kg)
匁 :1匁=10厘(約3.75g)
厘 :1厘=10毛(約0.375g)
毛 :1毛=10糸 原書文
注3-2:田の法3で割る
歩の単位の値を、畝や反の値に直すのに、30または300で割って求めることをいう。
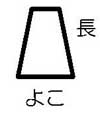
注3-3:長
四角形などの平面図形の場合、「長」といえば長い方の辺のことを指す。
注3-4:三角の法0.434をかける
1辺の長さが分かっている正三角形の場合、その1辺の長さの正方形の面積を出し、それにこの「0.434」をかければ、正三角形の面積が出る。つまり、正方形の面積から正三角形の面積を出すための「定数」
注3-5:円法0.79をかける
円の直径を1辺とする正方形の面積に、この「0.79」をかければ、円の面積が出る。つまり、正方形の面積から円の面積を出すための「定数」
原書文